강문진(왼쪽 두 번째) KAIST 수리과학과 교수가 연구원들과 함께 주먹을 쥐고 웃고 있다. 사진 제공=한국연구재단수학계에서 100여 년간 해결되지 않은 리만 충격파의 안정성에 관한 난제를 처음으로 증명한 젊은 과학자가 ‘이달의 과학기술인상’을 받았다. 압축성 오일러 시스템으로 불리는 이 문제는 1752년 오일러가 최초로 유도하고 19세기 열역학 이론의 바탕 위에서 정립된 비선형 편미분방정식이다.
이 방정식은 유체의 역학을 질량·운동량·에너지보존법칙의 기반 위에서 모델링하며 수학뿐 아니라 물리 등 다양한 과학 영역에서 광범위하게 사용된다. 2개 이상의 독립변수에 대한 미분방정식으로 소리와 열의 전파 과정, 전자기학·유체역학·양자역학 등에 활용된다.
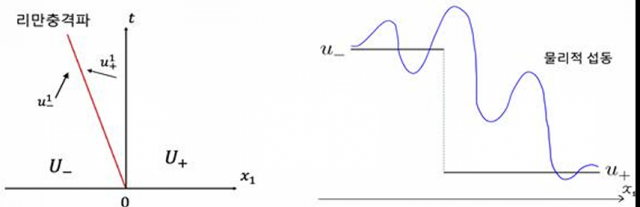
과학기술정보통신부가 주최하고 한국연구재단과 서울경제신문이 공동 주관하는 ‘이달의 과학기술인상’ 4월 수상자인 강문진(42) 한국과학기술원(KAIST) 수리과학과 교수는 공기와 같은 압축성 유체의 역학을 수학적으로 연구해 압축성 오일러 방정식의 충격파 문제를 1차원 공간에서 처음 해결한 공을 인정받았다. 이 충격파는 유체에서 전파되는 파동의 일종으로 음속보다도 빨리 전파돼 압력·온도·밀도 등이 급격하게 변화하는 게 특징이다. 초음속기가 음속을 돌파할 때 발생하는 소닉붐 등을 예로 들 수 있다. 압축성 오일러 방식은 매끄러운 초기함수로부터 발현된 해가 유한 시간 안에 충격파와 같은 불연속적이고 비가역적인 특이점을 생성하는 게 특징이다.
압축성 오일러 방정식의 충격파에 대한 난제 그림. 사진 제공=강 교수그동안에는 19세기 수학자인 리만이 제시한 자기 닮음 충격파가 물리적 교란에 의해 시간의 흐름에 따라 안정적으로 유지될 수 있는지에 대해 많은 수학자들이 답을 찾고자 노력했지만 해결하지 못했다. 특히 단순화된 형태의 리만 충격파의 초기 물리적 교란에 의한 안정성을 나비에·스토크스 방정식의 비점성 극한들의 집합 위에서 증명하는 문제는 완전히 숙제로 남아 있었다.
강 교수가 이 문제를 접한 것은 서울대 수학과에서 이학박사 학위를 받고 2013년 미국 텍사스대 오스틴캠퍼스의 알렉시스 바쇠르 교수 연구실에서 박사후연구원 과정을 밟을 때다. 당시 문제를 풀 수 있을지 장담하기 힘들었지만 세계적인 석학들과 공동 연구를 수행하며 몇 년 만에 문제 해결의 실마리를 찾았다. 1차원 공간 위에서 약한 리만 충격파가 물리적 교란에 의해 난류와 같은 불안정한 상태로 변하지 않고 안정적인 형태로 지속될 수 있다는 것을 이론적으로 규명했다. 이를 설명하기 위해 그는 1차원 공간 위에서 약한 리만 충격파의 물리적 안정성을 함의하는 새로운 방법론을 제시했다.
강 교수는 “이 방법론은 다차원 공간 위에서도 적용 가능한 아이디어들을 내포하며 맥스웰 방정식, 자기유체역학에 관한 방정식뿐 아니라 교통량과 혈액의 흐름, 에너지 재생 등 전혀 다른 현상을 모델링하는 현대수학의 편미분방정식 연구에도 적용될 수 있다”고 설명했다. 이어 “앞으로 압축성 오일러, 나비에·스토크스 방정식에 관한 미해결 난제들에 도전하겠다”고 밝혔다.
